Los triángulos son un patrón de corrección de cinco ondas (marcado como A-B-C-D-E), que se divide en cinco tipos. Este patrón se forma en una posición anterior a la onda final de un impulso o una corrección. Por ejemplo, podría formarse un triángulo en una cuarta onda en un impulso o en una onda B en un zigzag.
Además, este patrón se produce en la onda final X en un doble/triple zigzag o doble/triple tres.
La segunda onda de un impulso no puede ser un triángulo.
Las ondas A, B y C suelen ser zigzags, dobles zigzags, triples zigzags (es raro), dobles y triples tres.
Las ondas D y E podrían ser triángulos en sí.
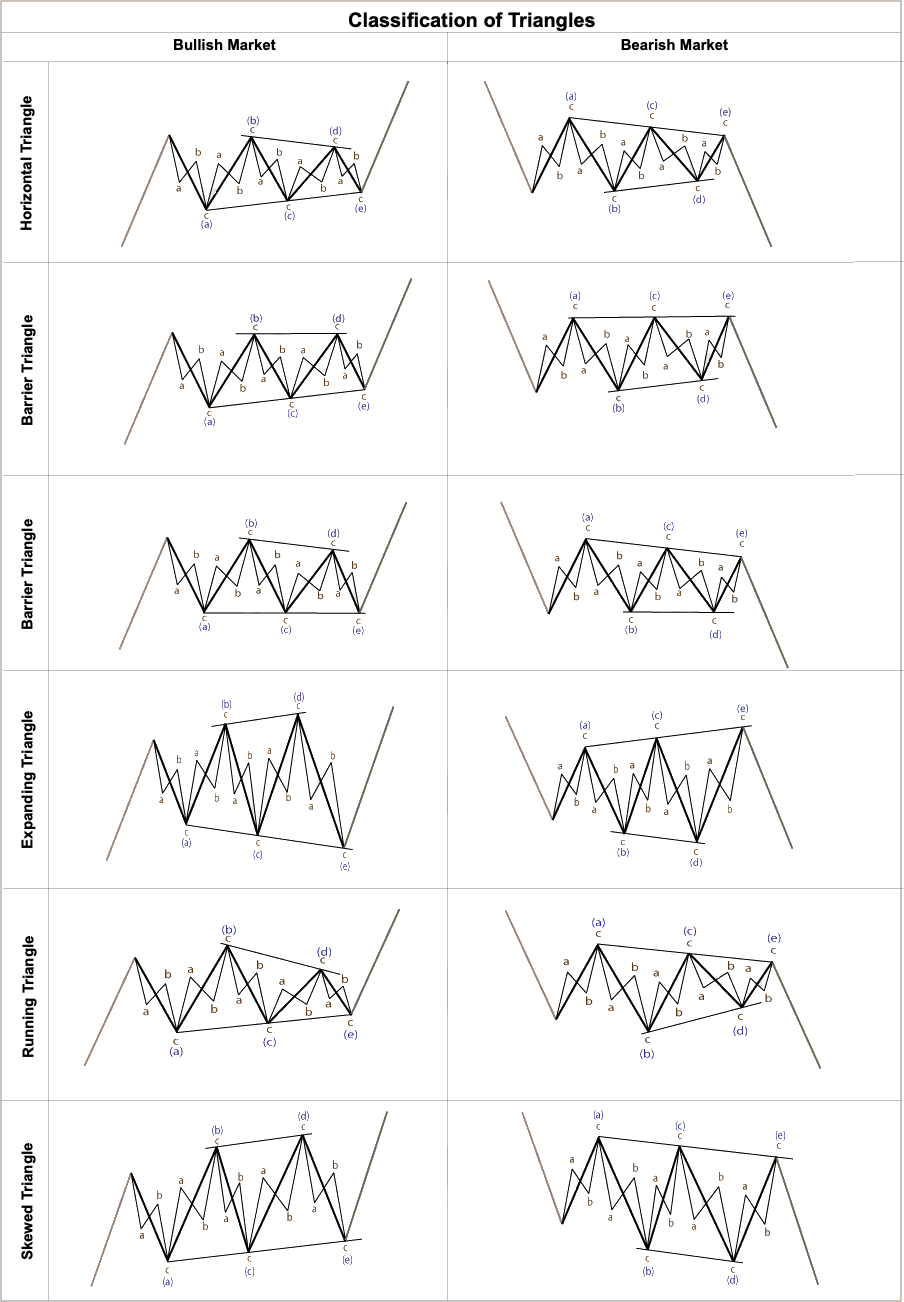
Clasificación de los triángulos
En la siguiente imagen, puedes encontrar todos los tipos de triángulos (horizontal, de barrera, expansivo, inclinado y en movimiento). Vamos a examinarlos uno por uno.
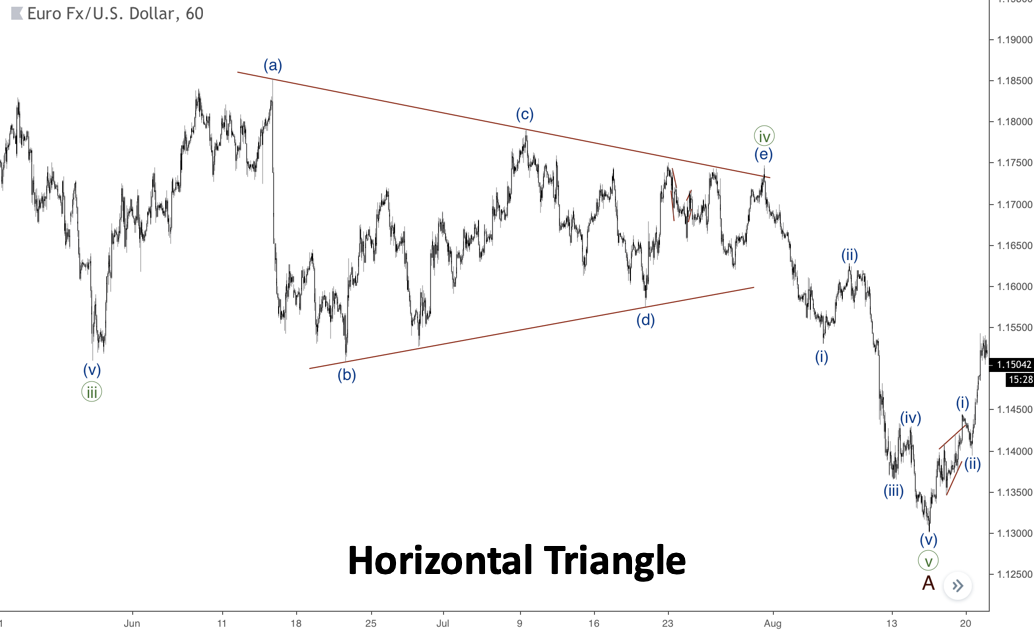
Triángulo horizontal
Este patrón también se conoce como triángulo contractivo. Como se puede adivinar por el nombre de este patrón, sus líneas se dirigen unas hacia otras. Cada onda de este triángulo es más corta que la anterior, lo que significa que la onda (b) no rompe el punto de inicio de la onda (a), la onda (c) no rompe el punto de inicio de la onda (b), etc. En el siguiente gráfico, se puede ver un triángulo en la posición de la cuarta onda, por lo que se produjo un descenso de la quinta onda justo después del patrón.
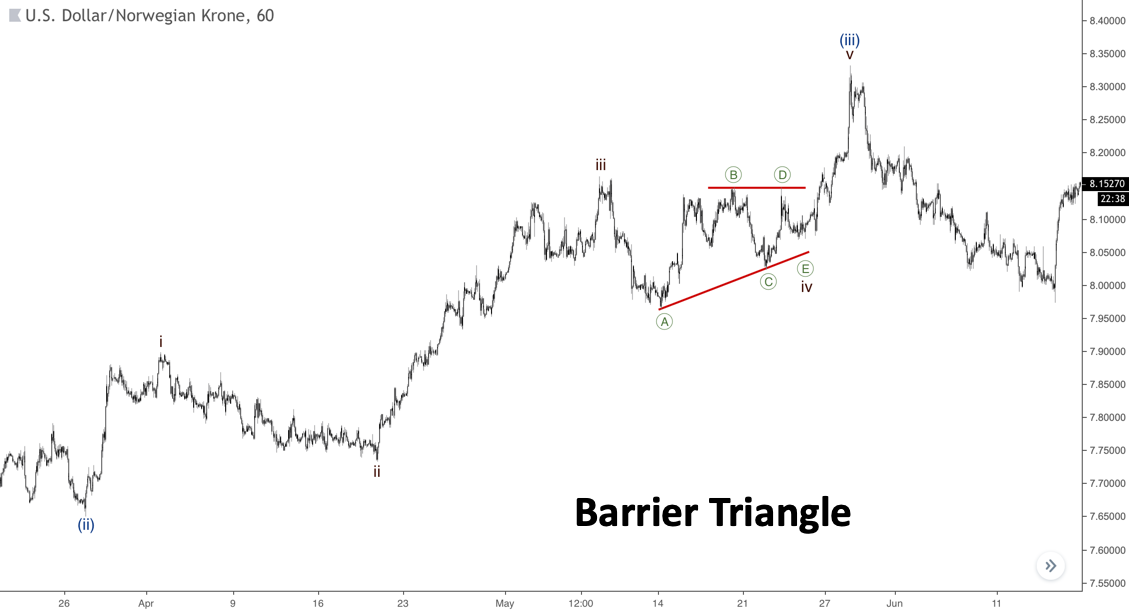
Triángulo de barrera
La única diferencia con el triángulo contractivo es que la línea B-D o A-C-E es horizontal. El otro va hacia una línea horizontal, por lo que un triángulo de barrera es una variación del patrón contractivo. Encontrarás un ejemplo de este patrón en el gráfico siguiente.
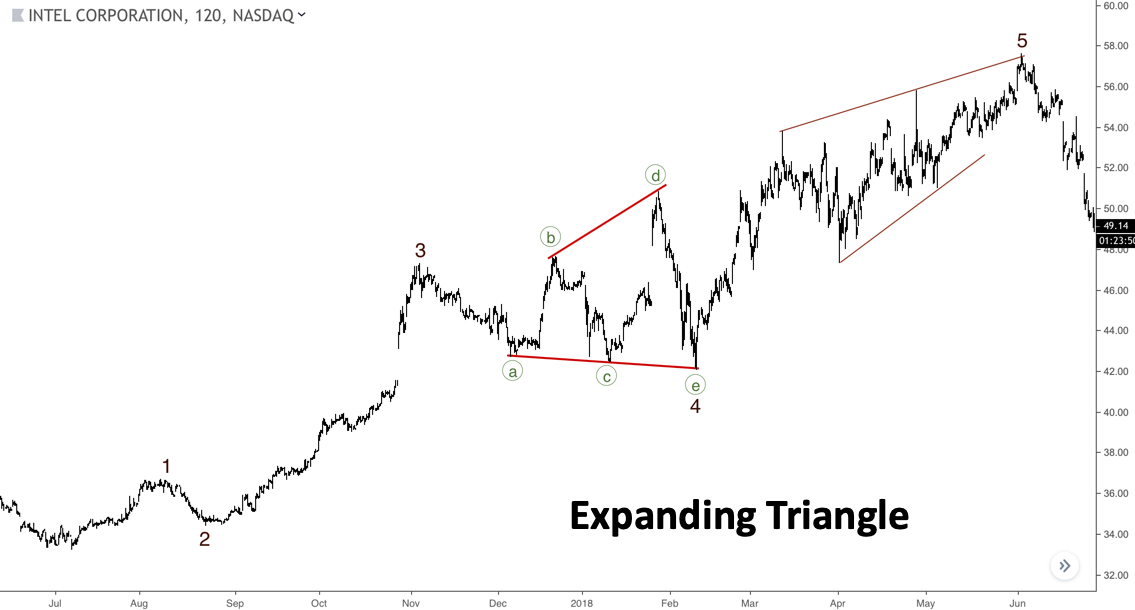
Triángulo expansivo
Este triángulo es el más complicado. Es simplemente imposible predecir este patrón desde el principio, por lo que podríamos contarlo solo cuando termine la onda E. Ambas líneas del patrón se dirigen en dirección opuesta.
Triángulo en movimiento
A veces, la onda B de un triángulo puede ser más larga que la onda A, pero todas las demás ondas son más pequeñas que la anterior. El siguiente gráfico muestra un ejemplo de triángulo en movimiento en la posición de la cuarta onda. Como se puede ver, la onda ((e)) del patrón no alcanza la parte superior del triángulo. Esto ocurre con bastante frecuencia, por lo que siempre debemos tener en cuenta la estructura de la onda E para predecir su final.
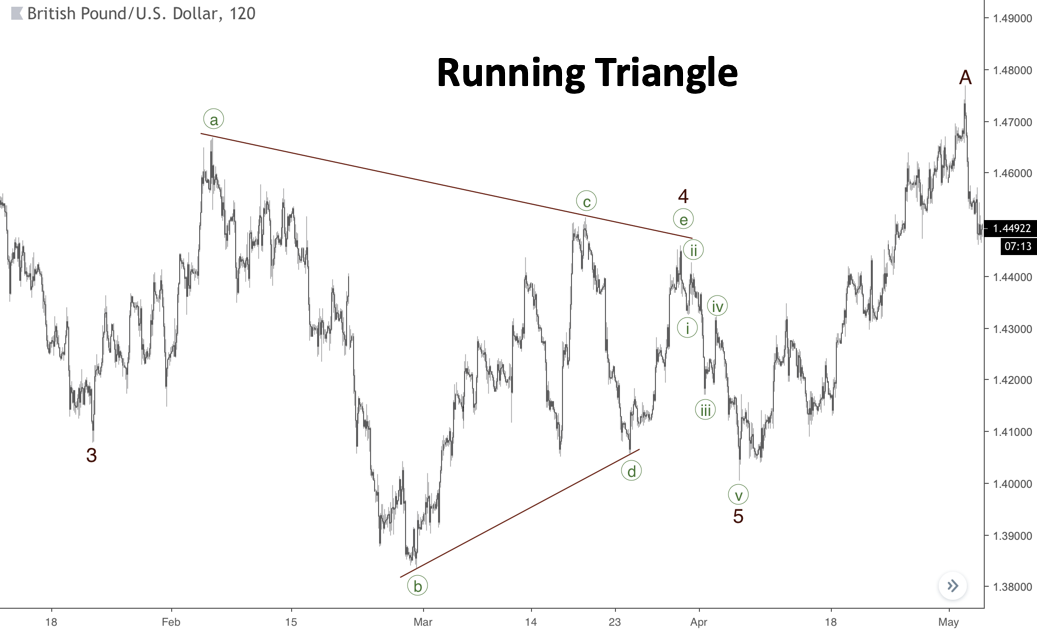
Triángulo inclinado
Si se produce una tendencia muy fuerte, podríamos enfrentarnos a un triángulo inclinado. Su onda D es más larga que la onda B, por lo tanto, es el único tipo de triángulo que tiene una dirección hacia la tendencia principal. Este patrón es poco frecuente y deberíamos marcarlo como el último escenario posible. El siguiente gráfico representa un triángulo inclinado, que impulsó el precio al alza en la quinta onda.
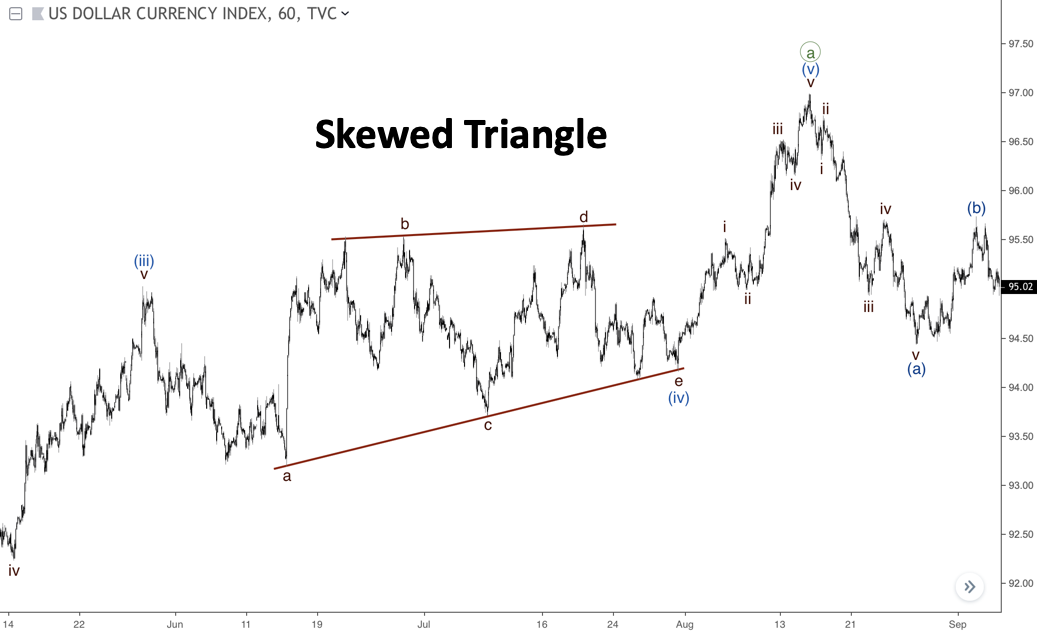
Otros ejemplos: fin de la onda E
Es posible que la onda E rompa la línea A-C de un triángulo. Si esto ocurre, es importante esperar a que el precio vuelva al rango del patrón. Como se puede ver en el gráfico a continuación, el par probó la parte inferior del triángulo, pero un posterior retroceso de la misma dio lugar al inicio de la quinta onda.
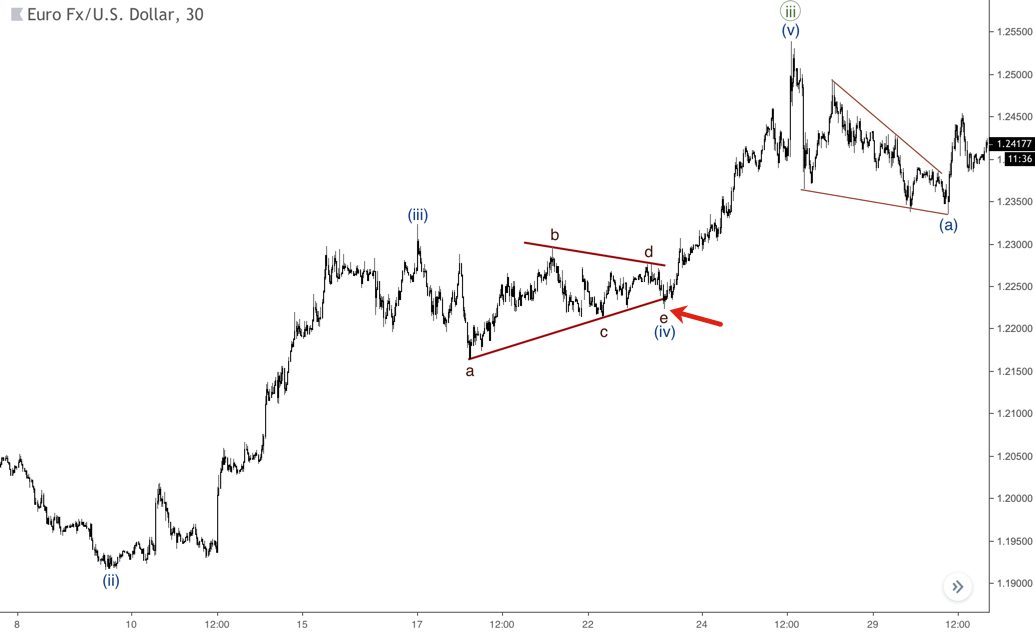
Quinta onda masiva
De vez en cuando, el mercado puede moverse bastante rápido justo después de un triángulo. El siguiente gráfico muestra ese caso. El final de la onda ((iv)) como un triángulo se convirtió en un enorme rally en la onda ((v)). Como sabemos que un triángulo se forma antes de la onda final de un impulso, deberíamos esperar una corrección tras el rally. Observamos que también hay un pequeño triángulo en la onda (iv) de ((iii)).
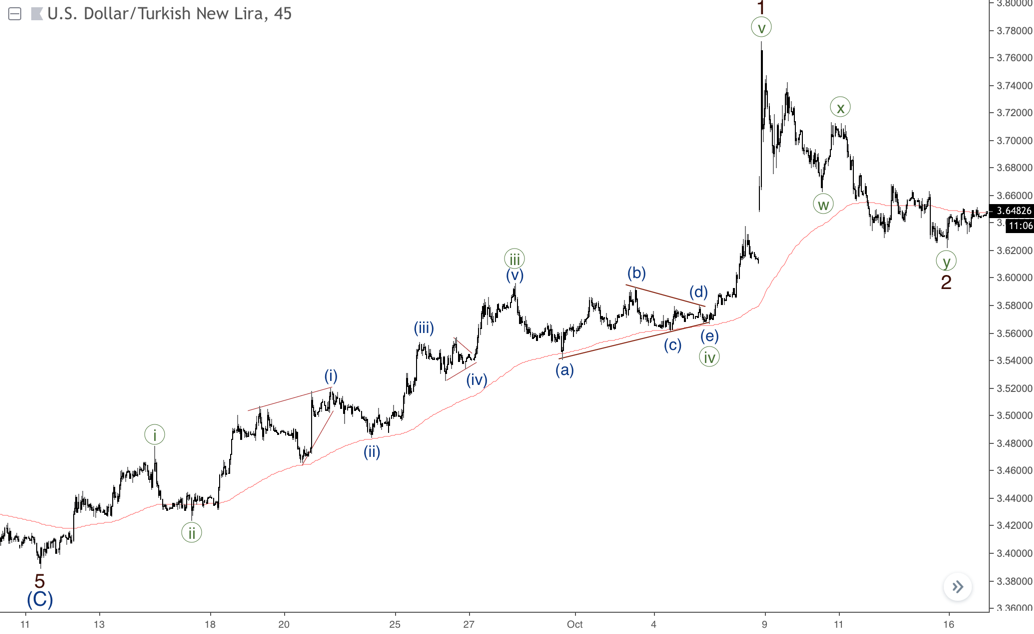
Dos triángulos
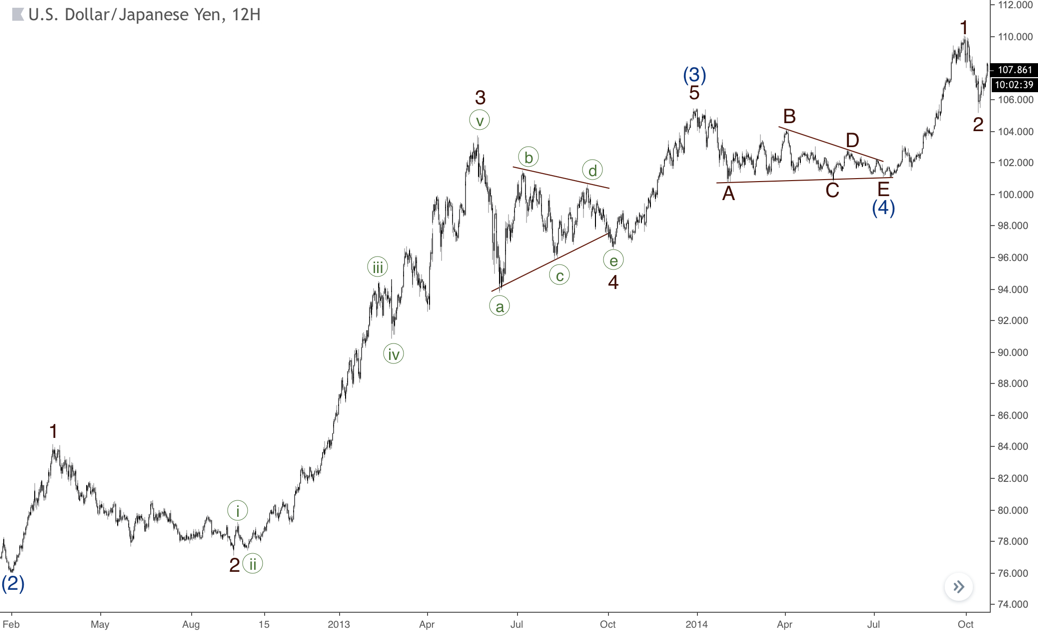
Si se produce una extensión en la tercera onda, es posible que se formen dos triángulos seguidos, que podrían formarse en una posición de la cuarta onda desde diferentes grados. Puedes encontrar un ejemplo de este caso en el último gráfico. La cuarta onda de (3) se forma como un triángulo, pero justo después de la quinta onda de (3) el mercado desarrolló otro triángulo en la onda (4).
En resumen
Hay varias formas diferentes de triángulos. Este patrón es la última corrección en estructuras impulsivas o correctivas. Podríamos contar un triángulo solo cuando su estructura esté totalmente terminada.